Interest Rate Model (IRM)

Configure utilization-aware interest dynamics

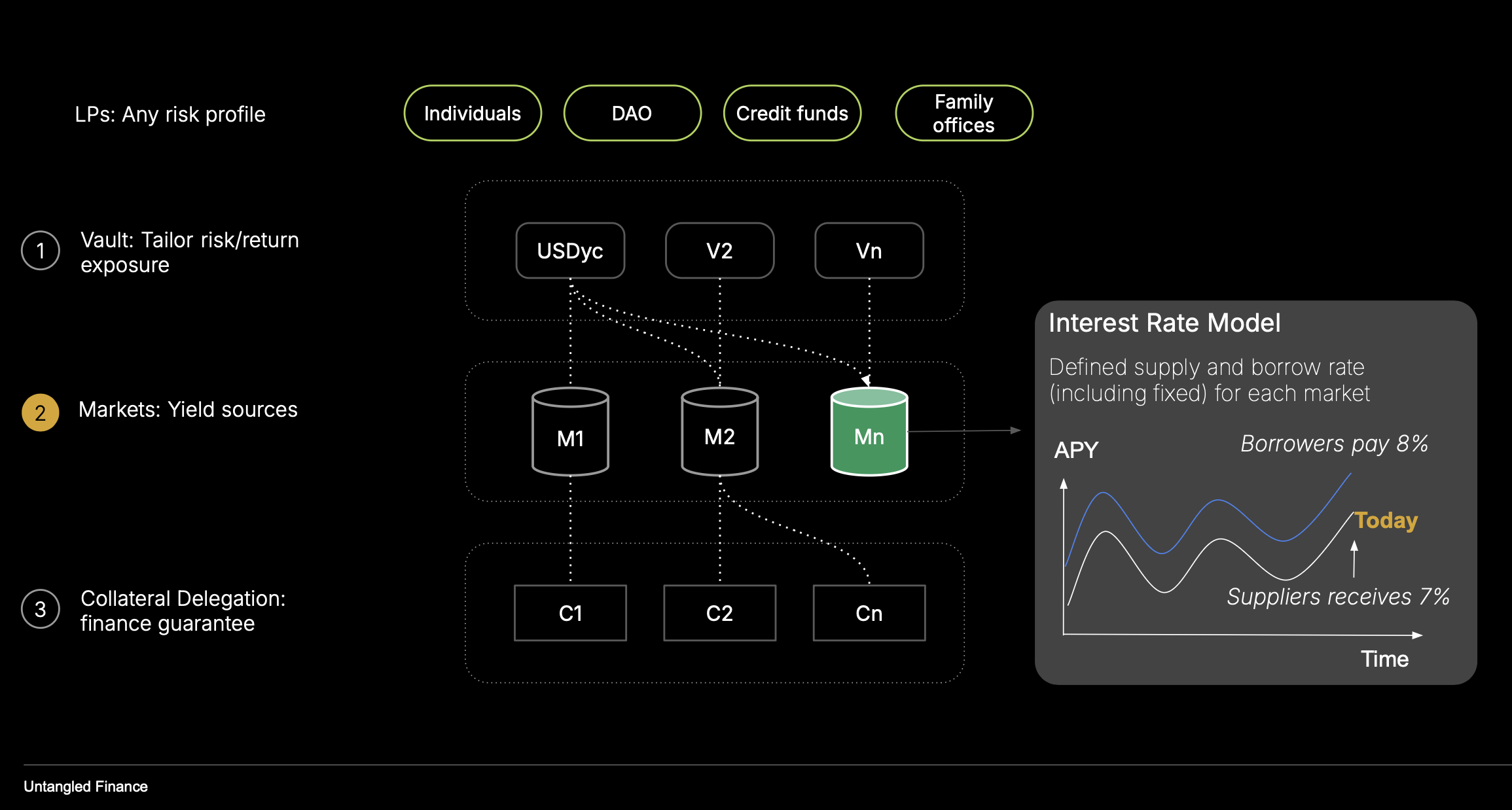
Overview

OctoLend’s Interest Rate Model (IRM) governs how borrowing costs evolve over time, targeting liquidity resilience across market conditions.

The model combines:

• A utilization-linked baseline (linear floor).
• A stabilizing integral term around an optimal utilization.
• An adaptive penalty that accelerates rates above a critical utilization threshold with time-dependent memory.
• A low-utilization dampener to avoid overpricing when markets are underused.

The IRM produces both:

• an instantaneous annualized borrow rate (for pricing and monitoring), and
• a compounded effect over time (for total debt growth and debt-share pricing).

Rates are anchored to a linear utilization floor, stabilized around an optimal target, and escalated dynamically above a critical threshold with stress memory that decays as conditions normalize.

By pairing instantaneous pricing with explicit compounding, the IRM balances liquidity, predictability, and responsiveness—key for institutional-grade lending on OctoLend.

Purpose

The IRM is designed to keep markets liquid and predictable:

• Encourage repayments or fresh supply when utilization is high.
• Avoid punitive rates when utilization is low.
• Stabilize around a curator-defined optimal utilization (set at market initialization).
• React quickly during stress while decaying back as conditions normalize.

This aligns market liquidity with LP withdrawals and protects lenders from prolonged max-utilization states.

What the IRM Controls

• Instantaneous borrow rate (annualized): Derived from current utilization and internal state.
• Compounded growth: Continuous compounding of total debt assets between accruals.
• Debt price: Value per debt share used for accounting, repayments, and liquidation math.
• Internal adaptation variables: Stateful terms governing stress escalation and decay.

Key Parameters

Each market sets a one-time, immutable configuration. Parameters are expressed in fixed-point integers (WAD = 1e18) or integers/basis points as appropriate.

Parameter	Description
u_opt	Target (optimal) utilization around which the system stabilizes.
u_crit	Critical utilization above which stress penalties activate.
u_low	Low-utilization threshold enabling rate dampening.
k_lin	Baseline slope for linear utilization-linked rate (r_lin = k_lin × u).
k_i	Integral gain driving stabilization toward u_opt.
k_crit	Penalty slope applied above u_crit.
k_low	Low-utilization slope shaping downward rate adjustment.
beta	Adaptation speed of stress memory (t_crit).
r_i	Stateful baseline rate component, updated on each accrual.
t_crit	Stateful stress-memory term; increases above u_crit and decays below it.

Parameters and bindings cannot be modified after market initialization.

Rate Dynamics

Linear Baseline

r_lin = k_lin × u

Borrow rates scale linearly with utilization, establishing a utilization-appropriate minimum rate.

Integral Stabilization around u_opt

The internal baseline r_i evolves over time based on (u − u_opt):

• If utilization > u_opt, r_i increases.
• If utilization < u_opt, r_i decreases, but never below r_lin.

This integral action gently steers utilization back toward the target.

Stress Penalty above u_crit

When utilization exceeds u_crit, a stress penalty activates:

• Stress memory (t_crit) accumulates the longer utilization remains above u_crit.
• As t_crit grows, rates escalate to attract liquidity or force deleveraging.
• Once utilization falls back below u_crit, t_crit decays at a rate controlled by beta.

Low-Utilization Dampener

When utilization drops below u_low, a bounded negative adjustment reduces rates to keep borrowing attractive in underutilized markets.

Putting It Together

All components are combined as: r = max(r_lin, r_i + r_p)

The resulting per-second rate is scaled to an annualized rate for reporting and monitoring.

Compounding and Accrual

Between accrual timestamps, the IRM integrates the evolving rate to compute compounded debt growth:

1. Approximates the rate path between the last accrual and the current timestamp.
2. Integrates and exponentiates the rate to obtain a compounded growth factor r_comp.
3. Applies the factor to total debt assets:
   total_debt_assets = total_debt_assets × (1 + r_comp)

This mechanism captures both gradual stabilization and rapid stress-driven escalation.

Debt Price and Debt Shares

The IRM exposes a debt price used across the market:

• The debt price reflects compounded total debt assets relative to total outstanding debt shares.
• If no debt shares exist, a fixed initial price is returned.
• As interest accrues, the debt price monotonically increases, ensuring consistent valuation for repayments and liquidations.

This provides transparent, on-chain insight into borrower liabilities and market health.

Initialization and Lifecycle

• The IRM is bound to a specific lending market at deployment.
• Configuration is immutable and can only be set once.
• On first use, the IRM initializes its internal state and accrual timestamp.

Each accrual:

1. Updates stress memory (t_crit) and baseline rate (r_i).
2. Advances the last accrual timestamp.
3. Compounds total debt assets using the newly computed growth factor.

Outputs

• Instantaneous rate (annualized): Current borrowing APR implied by utilization and IRM state.
• Compounded factor: Growth applied to debt since the last accrual.
• Debt price: Value per debt share used for accounting and liquidation.

These outputs expose liquidity pressure and verify IRM responsiveness.

Safety and Guardrails

• Rate floors: Borrow rates never fall below the linear utilization floor.
• Stress decay: Stress memory cools automatically as utilization normalizes.
• Deterministic math: Fixed-point arithmetic ensures predictable outcomes.
• Immutable configuration: Prevents mid-lifecycle governance drift.

What to Monitor

• Utilization: Compare current utilization against u_opt and u_crit.
• Stress memory (t_crit): Indicates persistence of stress conditions.
• Borrow rate vs. r_lin: Reveals active stabilization or penalty effects.
• Accrual cadence: Confirms compounding tracks utilization changes.
• Debt price evolution: Validates consistency between interest accrual and repayments.

Example Behaviors

Market Condition	Behavior
Quiet (u < u_opt)	Rates hover near r_lin; integral term nudges utilization upward.
Efficient (u ≈ u_opt)	Rates stable; small deviations corrected smoothly.
Stress (u > u_crit)	Penalty activates; rates rise rapidly; decay as utilization normalizes.

FAQs

Does the model support fixed rates?
The IRM configuration supports a wide range of behaviors through parameter selection. While the underlying model remains the same, parameters can be set to approximate fixed or near-fixed rate behavior at market creation.

Why not a single static kinked curve?
Static curves do not react to time under stress. OctoLend’s IRM introduces integral control and stress memory, enabling adaptive escalation and smoother normalization.

How often should accrual run?
Accrual may be triggered whenever meaningful time or utilization changes occur. More frequent accrual improves accuracy of compounding.

What happens at extremely low utilization?
The low-utilization dampener ensures borrowing costs remain attractive, preventing stagnation in underused markets.

Configurations

Utilization-Responsive (PI with Stress Memory)

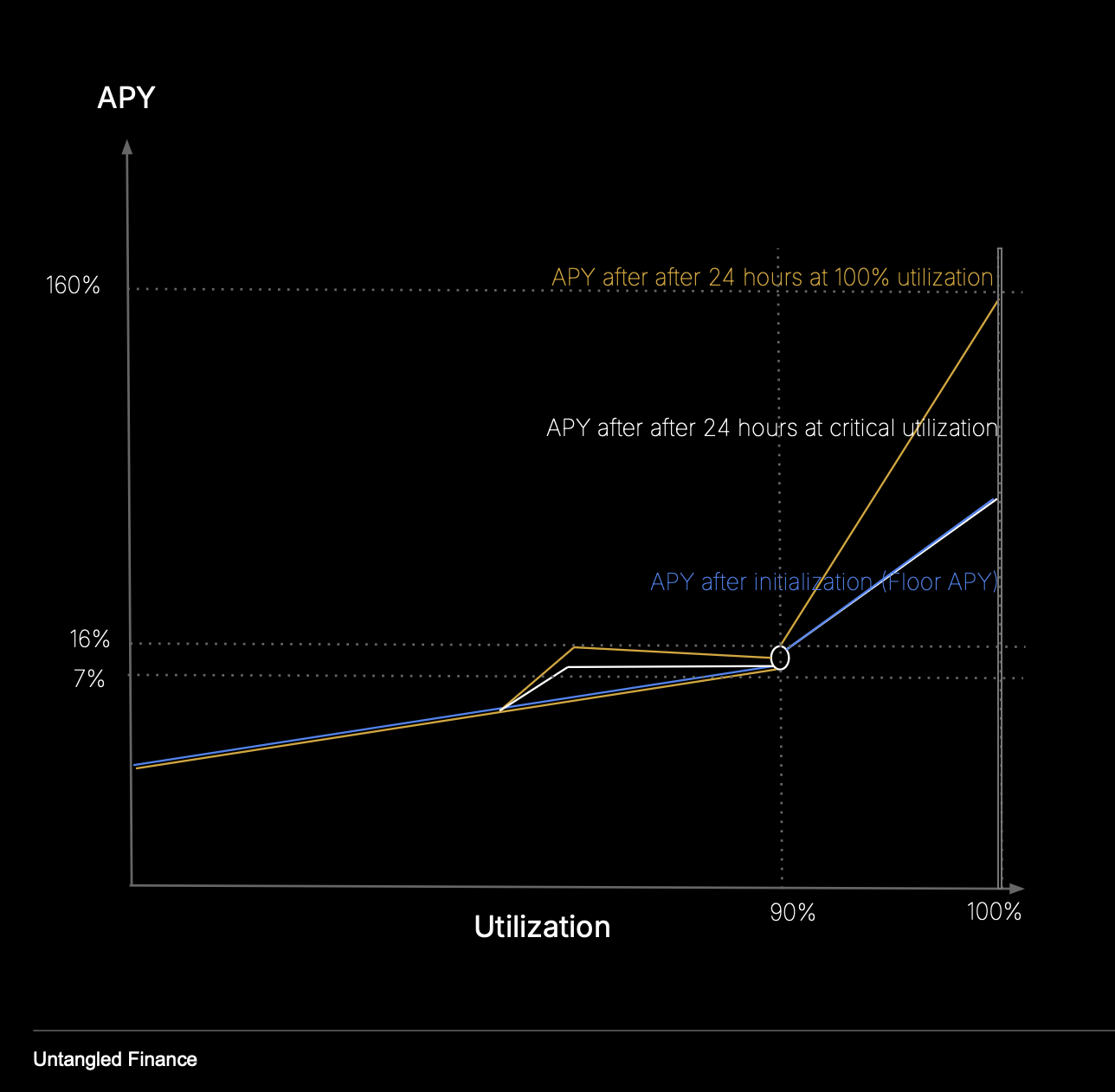
Defines an optimal utilization band with stable rates. Above it, stress memory and penalties activate to restore balance.

Linear Utilization

Rates scale primarily linearly with utilization, with reduced stabilization and penalty effects.

Near-Fixed

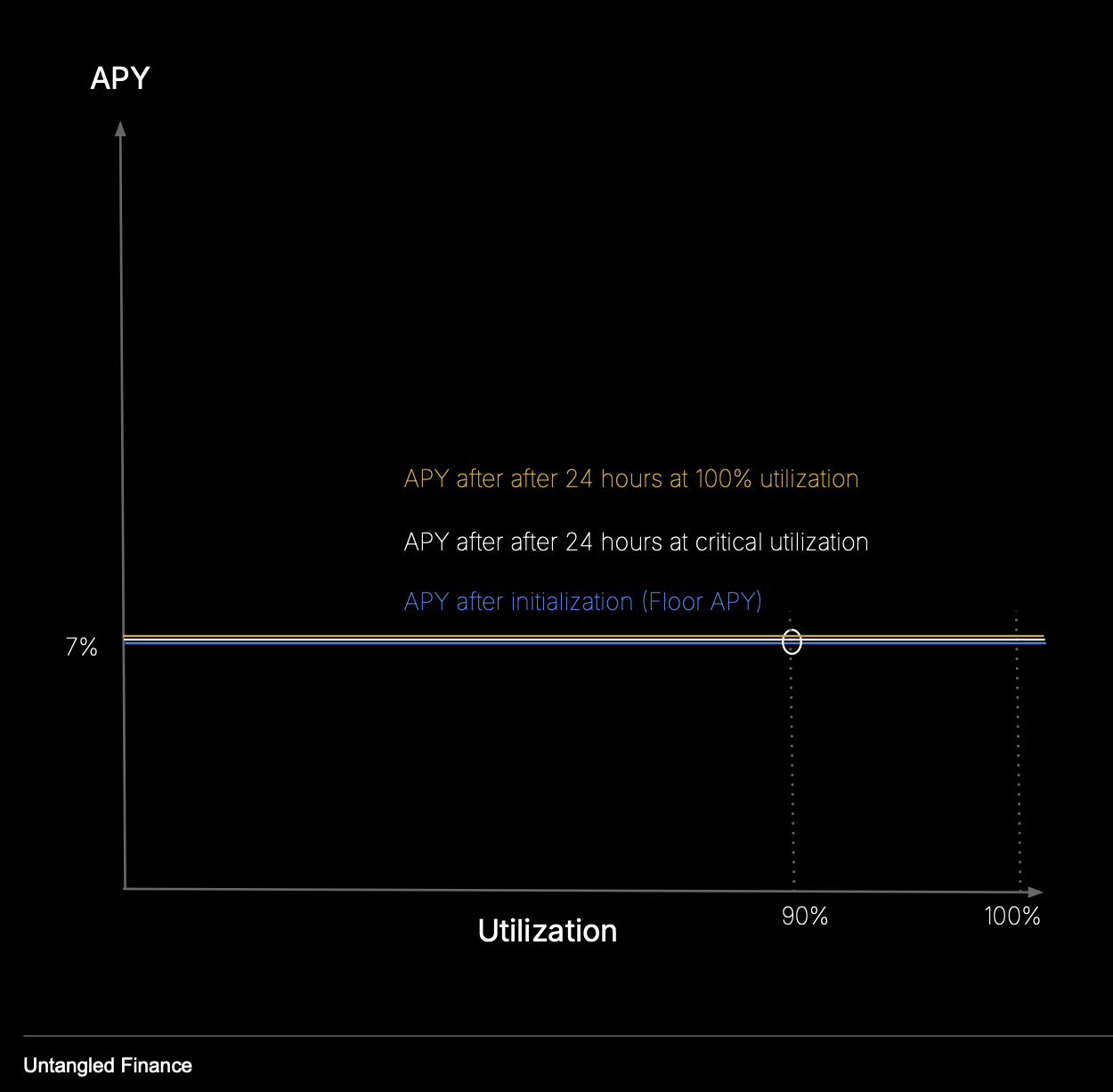
Parameterization that approximates a fixed-rate market across utilization levels, suitable for predictable or RWA-style lending.